Logic: The Rational Precondition – Geisler, N. L.

Logic deals with the methods of valid thinking; it reveals how to draw proper conclusions from premises. It is a prerequisite of all thinking, including all theological thought. Logic is such an inescapable tool that even those who deny it cannot avoid using it, for it is built into the very fabric of the rational universe.1
THE FUNDAMENTAL LAWS OF THOUGHT
There are three elemental laws of all rational thinking:
(1) the law of noncontradiction (A is not non-A);
(2) the law of identity (A is A);
(3) the law of excluded middle (either A or non-A).
Each of these laws serves an indispensable function in theology.
The Law of Noncontradiction
Without the law of noncontradiction we could not say that God is not non-God (G is not non-G). Thus, God could be the devil or whatever is anti-God.
The Law of Identity
If the law of identity were not binding, we could not say that God is God (G is G). Without the law of identity, God would not be identical to Himself; He could be something other than Himself (e.g., the devil), which is plainly absurd.
The Law of Excluded Middle
Likewise, if the law of excluded middle didn’t exist we could not affirm that it is either God or not God that we are speaking about. When we use the term “God,” we could be referring to both God and not God. This clearly is meaningless.
Hence these three principles are necessary for all thinking, including all thought about God. Since theology is thinking about God, theology cannot escape the use of these three fundamental laws of all thought.
A DEFENSE OF THE LAWS OF THOUGHT
Why should anyone accept these three laws? Indeed, many reject them, at least when applied to the ultimate level. Zen Buddhism, for example, claims that the Tao (the Ultimate) goes beyond all categories, including true and false (see Suzuki, IZB). How can the primary standards of thought be defended against such criticism?
Actually, the laws of thought are self-evident and do not need any defense. As regards the law of identity, for instance, the predicate says the same thing as the subject (A is A); therefore, it neither needs nor admits direct proof. Once one understands the terms, they speak for themselves. For example, once one knows what “triangle” and “three-sided figure” mean, there is no need to prove that a triangle is a three-sided figure. It is simply seen (by rational intuition) to be true.
However, there is an indirect way of defending the basic laws of thought as self-evident. This can be shown in that they cannot be denied without using them; that is, any attempt to deny them is self-destructive. It is like saying, “I think that I cannot think,” or “I know that I cannot know,” or “I reason that I cannot reason.” In each case, one is doing exactly what he claims he cannot do.
In the same manner, if the law of noncontradiction is not binding, then what is true can also be not true (false). But this is self-defeating, for that very sentence claims to be true and not false. If it does not claim to be true, then it is not even in the arena of truth and can be ignored by all who seek truth.
THE LAWS OF RATIONAL INFERENCE
In addition to the three fundamental laws of thought, there are laws of valid inference whereby a conclusion can be properly drawn from given premises. These fall into two broad categories: deductive logic and inductive logic.
The validity of these laws is dependent on the law of noncontradiction, for if these necessary rational inferences are not valid, then contradiction follows (see the following example).
DEDUCTIVE LOGIC
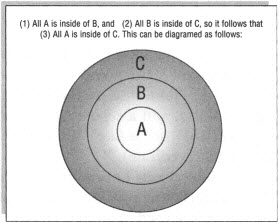
Deductive thinking is where one proposition is correctly deduced or drawn from others. For example, if:
(1) all A is inside of B, and
(2) all B is inside of C, then it follows that
(3) all A is inside of C.
If all A is not inside (in the class of) C, then contradiction follows, for then B would both be inside C (according to the second premise) and not inside C. If B is inside C, then A must be inside C, too, since A is inside B. Without question it is contradictory to both have and not have A inside of B (as according to the first premise).
The device by which one proposition can be correctly drawn from others is called a syllogism.2 Deductive logic comes in three forms:
(1) categorical syllogisms
(2) hypothetical syllogisms
(3) disjunctive syllogisms (see Aristotle, PrA and PoA).
Categorical Syllogisms
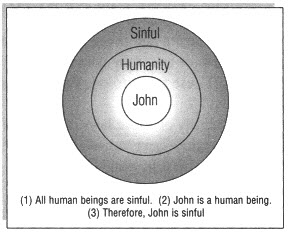
A categorical (unconditional) syllogism is one where a categorical (unconditional) proposition is deduced from two other categorical propositions. For example:
(1) All human beings are sinful.
(2) John is a human being.
(3) Therefore, John is sinful.
There are rules for categorical syllogisms that must be followed if the conclusions are going to be correct, and if these are not followed, then the undeniable law of noncontradiction is violated. These syllogistic rules and the fallacies that violate them can be understood if some of the essential terms are defined first.
Propositions
A proposition is a declarative sentence that affirms or denies something. A proposition is composed of a subject (the subject of the affirmation/ denial, e.g., “John”), a predicate (what is affirmed/denied of the subject, e.g., “sinful”), and a copula (the connector of the subject and predicate, e.g., “is (are)” or “is (are) not”). Stated together: “John (subject) is (copula) sinful (predicate).”3
The subject can be universal (including all in its class) or particular (specific, including only some in its class). For instance, “All dogs (universal) are four-legged creatures”; “some dogs (particular) are brown.” Universal propositions are said to be strong and particular ones weak. Propositions also can be either affirmative (“is” or “are”) or negative (“is not” or “are not”).
Combining universals and particulars with affirmatives and negatives yields four different kinds of propositions:
A Universal affirmative (All humans are sinners).
E Universal negative (All humans are not sinners) (or no humans are sinners).
I Particular affirmative (Some humans are sinners).
O Particular negative (Some humans are not sinners).
Distribution
In A-type propositions (universal affirmative) the subject is distributed and the predicate is not distributed.4 Take, for instance, a proposition similar to what we have just seen: “All human beings are rational.” The subject is distributed because “all humans” includes all in its class, and the predicate is undistributed because “rational” means only some of its class—there are, after all, other rational beings, such as God and angels.
The distribution (D) or undistribution (U) of terms in all four kinds of propositions is as follows:
A All S(D) is P(U).
E No S(D) is P(D); or All S(D) is not P(D).
I Some S(U) is P(U).
O Some S(U) is not P(D).
For example:
A All human beings (D) are rational (U).
E No human being (D) is rational (D).
I Some human beings (U) are rational (U).
O Some human beings (U) are not rational (D).5
Again, a categorical syllogism contains two propositions from which a third is deduced. The syllogism as a whole contains three terms: a subject term (ST), a predicate term (PT), and a middle term (MT). The subject and the predicate are the subject and predicate of the conclusion, and the middle term occurs once in each premise, along with one occurrence each of the subject and predicate. For example:
All humans (middle term) are lost (predicate term). [A-type proposition]
John (subject term) is a human (middle term).
Therefore, John (subject term) is lost (predicate term).
The Rules of Categorical Syllogisms
Breaking any one of the seven rules of categorical syllogisms leads to an invalid conclusion, meaning that the conclusion does not follow (non sequitur) from the premises regardless of whether or not the conclusion happens to be true.
(1) There must be only three terms.
(2) The middle term must be distributed at least once.
(3) Terms distributed in the conclusion must be distributed in the premises.
(4) The conclusion always follows the weaker premises (i.e., negative and particular ones).
(5) No conclusion follows from two negative premises.
(6) No conclusion follows from two particular premises.
(7) No negative conclusion follows from two affirmative premises.
The Fallacies of Categorical Syllogisms
Likewise, committing any one of the four fallacies of categorical syllogisms leads to an invalid conclusion.
(1) Illicit major is the fallacy where the major term is distributed in the conclusion but not in the premise.6
(2) Illicit minor is the fallacy where the minor term is distributed in the conclusion but not in the premise.7
(3) Undistributed middle is the fallacy where the middle term is not distributed at least once.
(4) Four-term fallacy is the fallacy where there are not three and only three terms in the syllogism (includes the fallacies of “ambiguous middle” and “equivocal middle”).
Of course, the middle term must appear only once in each premise but never in the conclusion; else, a fallacy of form occurs. A more detailed explanation can be found elsewhere (see Geisler and Brooks, CLUR).
Hypothetical Syllogisms
Hypothetical syllogisms are an “If … then …” type of reasoning. If A, then B follows. For instance,
(1) If God is all-just, then He must punish all sin.
(2) God is all-just.
(3) Therefore, He must punish all sin.
There are only two ways to draw valid conclusions from a hypothetical syllogism:
(1) affirming the antecedent (the part of the sentence coming before “then”);
(2) denying the consequent (the part of the sentence coming after “then”).
The above example (regarding sin and God’s justice) is one of affirming the antecedent (called modus pollens8), and the following is one of denying the consequent (called modus tollens9):
(1) If the Qur’an is God’s Word, then it cannot err.
(2) The Qur’an has errors.
(3) Therefore, the Qur’an is not God’s Word.
Disjunctive Syllogisms
A disjunctive syllogism is an either/or type of reasoning. It takes the following form:
(1) It is either A or not A (but not both).
(2) It is not non-A.
(3) Therefore, it is A.
To use a theological example:
(1) Either God is existent or He is nonexistent.
(2) God is not nonexistent.
(3) Therefore, God is existent.
There are two ways to draw a valid conclusion from a disjunctive syllogism: Either by denying one alternate or by denying the other alternate. An alternate is the statement on one side or the other of the “or.”
These three types of logical thinking—categorical, hypothetical, and disjunctive—are used constantly in theology. Without them theology would not be possible, since they are the rules of rational thought, and systematic theology is a form of rational thinking.
INDUCTIVE LOGIC
Another type of logic is inductive reasoning. While Aristotle wrote on inductive reasoning (T), he is more famous for deductive logic. Inductive and experimental logic were most fully developed by Francis Bacon (see NO), the father of modern scientific thinking, and John Stuart Mill (see SL).
The Nature of Inductive Reasoning
Broadly speaking, while deductive reasoning is from the general to the particular, inductive reasoning is from the particular to the general. For example, deductive logic proceeds from the general statement that
(1) all human beings are rational beings, and notes that
(2) Mary is a human being, to the particular conclusion that
(3) Mary is a rational being.
Inductive logic begins with any number of particulars and makes a generalization about them. For instance, “Human beings such as Janna, John, Joan, Jim, and others have two legs and walk upright; therefore, all humans walk upright.” Of course, unlike deductive logic, one cannot be absolutely sure of this conclusion, since all human beings have not been observed. Hence, the inductive conclusion is generalizing. It is a projection or extrapolation being made: “Since all humans we observe have two legs and walk upright, then even those we have not observed probably do the same.”
There is, of course, such a thing as a perfect induction, where every particular instance has been examined. In this case, one can be certain about the conclusion. For example, “Every coin in my pocket is a penny” can be known for sure, since my pocket is a limited space and every coin in it can be scrutinized. Likewise, the Bible contains a limited amount of information, all of which can be examined. Hence, one can have a kind of certainty about what it teaches if every verse has been probed carefully.
The Rules of Inductive Logic
Several inductive reasoning guidelines must be followed. Put in question form:
How Many Cases Were Examined?
The degree of certainty about the conclusion will depend in part on how broad was the number of cases examined. The broader the sample, the better the chances are that the conclusion will be correct.
How Representative Was the Evidence?
Since it is usually not possible to examine all the cases, the quality of the samples examined is crucial to the validity of the conclusion. For example, the validity of a poll will depend on the representative nature of the sum of the people who were polled.
How Carefully Was the Evidence Examined?
Careful inductions are comprised of many factors. What were the similarities of the samples that were studied? What were the differences? Were all possible explanations accounted for? Were the results isolated from other factors? In short, how critically was the evidence examined?
How Does the Information Gained Correlate With Other Knowledge?
Finally, how well does the information that was gleaned match up with other things that are known to be true? Does it contradict other things known with certainty? Does it better explain things than other explanations do? Sometimes new evidence rocks foundations that were thought settled (such as Copernicus’s view that the earth moved around the sun).
Kinds of Probability
There are two major kinds of probability in inductive reasoning: a priori (ah pree-oh-ree) and a posteriori (ah paw-ster-ee-oh-ree). A priori probability is probability prior to and independent of the facts; a posteriori probability is probability that arises after examining the facts. Both kinds have an application to theology and apologetics.
A Priori Probability
A priori probability is mathematical in nature, dealing with the advanced likelihood or odds of an event occurring. For example, the likelihood of getting three sixes on a roll of three dice before they are tossed is 1 in 216 (1/6×1/6×1/6). This does not mean that the dice must be thrown 216 times to get it; it simply means that these are the mathematical odds, for three dice with six sides numbered one through six offer that many combinations.
A priori probability has convinced even some former atheists to believe there must have been an Intelligent Designer of first life. After calculating that the odds for life to arise by only natural laws was 1 in 10 to the 40,000th power (one followed by 40,000 zeros), Sir Fred Hoyle (b. 1915) abandoned his God-denying beliefs. This chance, one in 1040,000, is less than that of finding one single particular atom while searching the entire universe (see EFS, 45–46).10
A Posteriori Probability
While a priori probability is probability before the fact, a posterior probability is probability after the fact. In science, it is empirical probability, also called scientific probability. A posteriori probability offers varying degrees of certainty that something is true based on an examination of the available evidence. This is generally done with the guidance of the principles listed above (under “The Rules of Inductive Logic”).
Degrees of Probability
According to the inductive method, there are various degrees of probability, depending on the kind and extent of evidence available. These range from virtually impossible on the one end to virtually certain on the other end. Absolute certainty, at least of a mathematical type,11 is possible only in deductive logic. A perfect induction, however, can provide practical certainty, since every one of the cases was examined.
LOGIC AND GOD
If logic is the basis of all thinking, and theology is thinking about God, then it follows that logic is the basis of all thinking about God. Nevertheless, some object to this conclusion, claiming that God is sovereign over all things, including logic, and that making logic the basis of thinking about God makes God subject to logic (see Dooyeweerd, NCTT).
Logic Is Subject to God Ontologically
It is true that in reality God is prior to everything else. In this sense, God is prior to logic in the order of being. Logic is a form of rational thought, and God is the ultimate rational Being. So ontologically,12 logic is subject to God.
However, this does not mean that logic is arbitrary—God does not merely choose to be rational and consistent. He is rational by His very nature. The Scriptures inform us, for example, “It is impossible for God to lie” (Heb. 6:18) and that “He cannot deny Himself” (2 Tim. 2:13 nkjv). Likewise, God cannot be irrational. It is contrary to His nature as the ultimate, perfect, absolutely rational Being in the universe to violate the laws of logic.
God Is Subject to Logic Epistemologically
While God is prior to logic in the order of being (ontologically), nevertheless, logic is prior to God in the order of knowing (epistemologically). No knowledge is possible without the laws of thought; if this is not true, then nothing else follows. Even the statement “God is God” makes no sense unless the law of identity holds (A is A). Likewise, the affirmation that “God exists” cannot be true if the law of noncontradiction is not binding, otherwise God could exist and not exist at the same time and in the same sense.
Is God subject to something beyond Himself? No. When God is subject to good reason (logic), He is subject to His own nature (see Clark, CVMT), since He is the ultimate Reason or Logos (John 1:1). Likewise, when God is subject to the law of justice, He is not bound by something beyond Himself but to something within Himself, namely, to His own unchangeable nature (see volume 2).
Technically speaking, in theology it is not God who is subject to logic; it is our statements about God that are subject to logic. Systematic theology is a series of statements about God that, if true, inform us about Him. No statement about God can make any sense, to say nothing of being true, unless it abides by the undeniable rules of reason.
Rationality or Rationalism?
Some object that making God subject to logic is a form of rationalism, since it makes truths about God subject to human reason. However, there is a difference between the use of good reason, which the Bible commends to discover truth (Isa. 1:18; Matt. 22:37; 1 Peter 3:15), and the use of rationalism to determine truth, which Scripture does not commend. Good reason does not subject God to finite minds but rather subjects our finite minds to His infinite Mind (2 Cor. 10:5; 1 Cor. 1:21).
Further, since we are created in the image of an infinitely intelligent God, it is not a form of rationalism to imitate His rationality. Rather, it is a way to express our love for Him (with all our minds) as Jesus commanded (Matt. 22:37).
Even special revelation cannot be known or communicated apart from logic. We could not distinguish between a revelation that is from God or one that is not from God without the law of noncontradiction. Nor could we determine which book was God’s of the many that claim to be (e.g., the Bible, the Qur’an, the Book of Mormon) without using our reason to examine the evidence.
Finally, note that reason is a means of discovering truth, whereas rationalism is an attempt at determining truth. Christian theology falls into the former category. All truth is revealed by God, whether in special or general revelation (see chapter 4), but all truth is received by reason.
DID ARISTOTLE INVENT LOGIC?
Some critics object to the use of deductive logic, insisting that it was invented by Aristotle and that there is no reason we should accept “Western logic” over “Eastern logic,” which does not accept the law of noncontradiction.
However, this criticism is misdirected for several reasons. First, Aristotle did not invent logic; at best, he simply discovered it. All rational creatures were using logic since the beginning; Aristotle was merely the first one known to put it down in written form (see PrA and PoA).
Second, this criticism implies that “Eastern thought” can somehow avoid using “Western logic.” But this is impossible—logic does not have geographic boundaries. Inasmuch as logic is based on the law of noncontradiction, it is unavoidable, for it is impossible to deny this law without using it. Any statement to the effect that “truth claims do not have to be either true or false” is itself claiming to be true as opposed to false.
Third, no Eastern philosopher can even think without the law of noncontradiction; again, the very denial of noncontradiction employs it, and any statement to the effect that “ultimate reality [say, the Tao] goes beyond, the law of noncontradiction” (see Suzuki, IZB) is itself a statement that uses the law of noncontradiction of ultimate reality, for it claims to be true, as opposed to false. If it is not a truth claim at all, then it is not even in the arena of truth and need not be considered by anyone in pursuit of truth.
Are There Different Logics?
Others object that there are many kinds of logic; why choose one and make it the norm over all others? In response, it should be pointed out that there are no kinds of logic that do not use the law of noncontradiction. All systems of valid thought—whether they are deductive logic, inductive logic, symbolic logic, modal logic, or whatever—employ the law of noncontradiction. Indeed, Alfred North Whitehead and Bertrand Russell demonstrated in Principia Mathematica that all mathematics is based on logic. It is literally impossible to think without logic.
Can’t an Omnipotent God Break the Laws of Logic?
Some theologians argue that if God is omnipotent, then He can do anything, including breaking the laws of logic. The Bible says, “Nothing is impossible with God” (Matt. 19:26), and if this is so, it is suggested, it would seem to follow that God could violate the laws of thought if He wished.
However, this objection is based on a misconception. When the Bible declares that God can do anything, it does not mean that He can do what is impossible. It means that God can do anything that is possible to do. Indeed, the Scriptures declare that there are many things that are impossible for God. Hebrews 6:18 affirms, “It is impossible for God to lie”; 2 Timothy 2:13 nkjv adds, “He cannot deny Himself.” It would be a denial of Himself for God to deny the laws of rational thought, since they are based on His rational nature.
Can’t God Transcend Logic As He Does Natural Law?
Some have suggested that since God made natural law and can transcend it by supernatural intervention, it would seem to follow that He can do the same with the rational laws He has made. In short, if God can break His laws of physics, why can’t He break His laws of rationality?
The response to this is that God did not make or create the laws of thought any more than He created Himself. The laws of reason are based on God’s uncreated nature. That is the way He is, always has been, and always will be. God cannot change His nature and, hence, cannot break the laws that flow from His nature. The laws of physics are created, not uncreated, and can be transcended by God like everything else that is created. But as the laws of thought are based on God’s uncreated nature, God can no more change them than He can cease to be God.
Are Not the Mysteries of the Faith Against Logic?
From inside Christian theology, several other objections have been set forth flowing from the great mysteries of the faith: The Trinity, the Incarnation, and the doctrine of predestination/free will.
The Trinity
The orthodox view of the Trinity posits that there is only one God and yet three different Persons make up that one God. This appears to some to violate the law of noncontradiction; how can God be only one and yet three at the same time and in the same sense?
Put in this way, the answer is that He cannot, but this misstates the doctrine of the Trinity. According to evangelical theology, God is not both three and only one in the same sense. He is only one in nature (essence) but three in a different sense—in Persons.
Three persons in one essence is no more a contradiction than are three corners on one triangle or three ones in one to the third power (1×1×1=1). God has one what (nature) with three whos (persons). This is a mystery (cf. 1 Tim. 3:16) but not a contradiction. To be contradictory God would have to be both three and only one at the same time and in the same sense; that is, He would have to be three Persons and yet only one Person at the same time and in the same sense. Or, He would have to be three Natures and yet only one Nature at the same time and in the same sense. But this is not what orthodox theologians claim about the Trinity.
The Incarnation
Like the Trinity, the Incarnation is also a great mystery. Some even claim it is a contradiction, for it affirms that in Christ God became man, and this is impossible, since God is infinite and man is finite—an infinite cannot become finite. The Eternal cannot become temporal any more than the Uncreated can become a creature. How then can we claim that the Incarnation does not violate the law of noncontradiction?
The answer to this apparent contradiction lies in the misstatement of what the Incarnation really is. It was not God becoming man, but the second person of the Godhead adding humanity; in other words, the Son of God did not stop being divine in order to become human, but rather He embraced another nature—humanity—in addition to His divinity. In the Incarnation, the infinite nature of God did not become finite; the second person of the Godhead, who retained His infinite nature, also assumed another nature (a finite one). As we put it before, in God there is one what (nature) and three whos (persons).
In the Incarnation, Who2 took on What2, a human nature, in addition to the What1 He retained (His divine nature). This is not a contradiction because the infinite did not become finite, nor the Uncreated become the created, which would be a contradiction.
In the Godhead there is one What and three Whos; in Christ, the second person of the Godhead, there is one Who and two Whats. In the Incarnation, one Who in God assumed another What, so that there were two Whats (natures) in one Who (person). Again, this is an amazing mystery but not a contradiction.
Predestination and Free Will
For everyone except extreme Calvinists (see volume 3), who deny free will in this matter, or extreme Arminians, who deny God’s infallible fore knowledge, there is a seeming paradox between God’s predetermination and human free choice. How can God determine the end from the beginning (Isa. 46:10), and how could He have chosen His elect before the foundation of the world (Eph. 1:4), when the Bible also affirms that human beings are free to accept or reject God’s gift of salvation (John 1:12; Rom. 6:23; Matt. 23:37; 2 Peter 3:9)? If God determined in advance who will be saved and who will not be saved, then how can humans be free (see volume 3)?
The answer to this apparent dilemma resides in an understanding of how God predetermines events like these. God does not force them to happen against our free will; rather He predetermines that they will occur through our free will. Or, to put it minimally, God does not have to make these events occur; He can see them occur—from His eternal vantage point.13
A person standing on top of a building foreseeing a collision (between two cars that cannot see each other around the corner) does not cause the crash. Likewise, God, who can by His omniscience foresee what we will freely do, need not cause us to do it. And even if He is the ultimate cause of all things, He is not the immediate cause of them. Free moral agents are the immediate cause of all free actions. God (the primary cause) produced the fact of freedom, and free agents (secondary causes), by God’s grace, produce the acts of freedom (see volume 3).
Further, one and the same event can be both determined and yet free with no contradiction. For example, when one watches a recording of a televised game, it is already determined; nothing can be changed. It will turn out exactly the same, score and all, no matter how many times one watches it. Yet when the game was played, each and every person played according to his or her own free will. No one was forced to do anything. Thus, one and the same events were both determined and yet free (see Geisler, CBF, chapters 1–3).
To the objection that this is so because we are looking back on the game, the theist could reply, “God in His omniscience looks forward with an even greater certainty than we look backward.” This leads to another point.
The God of orthodox theology is eternal, not temporal. Therefore, He does not really look forward to the future; He simply looks downward on it (see volume 2), since it is present to Him in His eternal now (as the great I AM of Ex. 3:14). To illustrate, a person in a cave can look out the tunnel and see only one train car going by at a time—the present one. He cannot see the one already past or the one yet to come. But the person on the top of that mountain can see all of them at the same time. Likewise, God can see past, present, and future all in His eternal present (the now). He sees the future, not because it has already occurred, but because it preexists in Him as the eternal Cause of all that was, is, and will be.
If God is eternal, there is no problem with an event being determined in advance (and, thus, not being free), for then God is actively seeing in His eternal present what we are freely doing. He is not passively seeing the future (as though He had to wait on it to occur). He is not literally foreseeing anything. It is only called foreseeing and predetermining from our standpoint in time, not from God’s vantage point in eternity.
In point of fact, God knows the future not because He is looking down or ahead; He is simply looking within Himself, for all effects preexist in their cause,14 and God is the Cause of all things, including the future.15 Hence, God is seeing them in His eternal nature, before they ever occur, with the same certainty as if they had already occurred (see Aquinas, ST, 1a.14.6–9). There is no contradiction between God’s predestination and our free will.
Finally, the harmony between predestination and free choice can be demonstrated from God’s omniscience alone. Consider the following argument:
(1) God is all-knowing.
(2) An all-knowing Being knows everything, including the future.
(3) What an all-knowing Being knows will come to pass—must come to pass (if it did not, then God would have been wrong about what He foreknew. But an all-knowing God cannot be wrong about anything He knows).
(4) God knows all future free acts.
(5) Therefore, these free acts must come to pass. (If they didn’t, then an all-knowing God would have been wrong.)
(6) But what must come to pass is determined.
(7) Therefore, our free acts are predetermined by God.
While the logic of this argument is tight, many believe that it proves we aren’t free. This is not the case. What it demonstrates is that God can know for sure (has determined) what we will freely do. So one and the same event is determined from the standpoint of God’s knowledge and free from the vantage point of our choice. Again, this may be a mystery, but the great mystery of predestination and free will, whatever else it is, is not a logical contradiction.
CONCLUSION
Systematic theology is dependent on logic in many ways. All of its claims are subject to the basic laws of thought. Contradictions cannot both be true and false. Likewise, as will be seen in chapter 12, the methods used in doing systematic theology are both deductive- and inductive-type logic. Systematic theology begins with an inductive study of both special revelation (in the Bible) and general revelation (in nature), it makes deductions from them, and these are put together in a unified and systematic whole. Without logic, this would not be possible; hence, philosophy (especially logic) is truly the handmaid of theology.
SOURCES
Aristotle. Posterior Analytics.
———. Prior Analytics.
———. Topics.
Bacon, Francis. Novum Organum.
Clark, Gordon. A Christian View of Men and Things.
Dooyeweerd, Herman. New Critique of Theoretical Thought.
Geisler, Norman. Chosen But Free.
Geisler, Norman, and Ronald Brooks. Come, Let Us Reason: An Introduction to Logical Thinking.
Hoyle, Sir Fred. Evolution From Space.
Mill, John Stuart. System of Logic.
Suzuki, D. T. An Introduction to Zen Buddhism.
Thomas Aquinas. Summa Theologica.
Whitehead, Alfred North, and Bertrand Russell. Principia Mathematica.
1 For a more extensive treatment of logic, see Norman Geisler and Ronald Brooks, Come, Let Us Reason: An Introduction to Logical Thinking.
2 As mentioned in chapter 2, a syllogism, formally, is a deductive scheme of a formal arrangement consisting of a major and a minor premise and a conclusion (Webster’s Third New International Dictionary).
3 Each of the three statements of the syllogism is a proposition.
4 That a subject or a predicate is “distributed” means all in its class are included.
5 The subject of an A-type proposition is distributed because, for instance, “all human beings” means everything in that class; the predicate is undistributed because humans are only some of the rational beings that exist—others in that class include God and angels. The subject of an E-type proposition is distributed because “no” equals “all”; the predicate is likewise distributed, specifically, since no human being is in the class of any (all) rational beings. In an I-type proposition, both subject and predicate are undistributed because the statement means that some humans are in the class of some rational beings; again, there are others who fall into the class labeled “rational.” The subject of an O-type proposition is undistributed because it refers only to some human beings; the predicate is distributed because it negates all in that class—that is, some human beings are not in the class of any (all) rational beings.
6 The “major term” comes from the major premise and contains the predicate of the conclusion.
7 The “minor term” comes from the minor premise and contains the subject of the conclusion.
8 Latin for “method of affirming.”
9 Latin for “method of denying.”
10 Of course, there are factual observations used in this calculation, such as the age of the universe and the rate of mutations, etc.
11 Moral certainty is possible, as it is not based on deductive logic but on moral, psychological, and/or spiritual factors. For example, God can grant moral (or spiritual) certainty of salvation (Rom. 8:16) where the actual evidence itself may justify only a probable conclusion (see volume 3).
12 Ontology is the study of being.
13 This does not mean God sees them in a passive sense. He sees them actively and chooses them eternally. Hence, His knowledge is causal, for the future preexists in God as the Cause of all things that have occurred, are occurring, or will occur.
14 Effects preexist in their cause because an efficient cause cannot give what it does not have. It cannot share with another what it does not have to share; it can only produce what it possesses (see chapter 9).
15 God is the Cause of all that exists, but He causes it from eternity, where He alone exists. Even time—having had a beginning—is caused by the eternal God. All events in time caused by God were caused from eternity, even though the effect does not occur until a specific time. Of course, since evil is a privation or corruption of being, God is not the cause of evil. He is the cause of the good being in which the parasite of evil has taken residence.
Geisler, N. L. 2002. Systematic theology, volume one: Introduction, Bible (81). Bethany House Publishers: Minneapolis, MN